5  Discriminant analysis

Discriminant factor analysis (DA) or simply discriminant analysis is a statistical technique that aims to:

the membership to predefined groups (classes, modalities of the variable to be predicted…) of a set of observations (individuals, examples…) from a series of predictive variables (descriptors, exogenous variables…).

In medicine, to detect high-risk cardiac groups based on characteristics such as diet, smoking or not, family history, …

Discriminant analysis can be a descriptive technique:

Discriminant analysis can be a predictive technique:

5.1 Principle

We have a sample of \(n\) observations distributed in \(K\) groups of sizes \(n_k\). The number of classes \(K\) is fixed in advance.

\[\begin{aligned} X_n = \begin{bmatrix} x_{11} & x_{12} & x_{13} & \dots & x_{1p} \\ x_{21} & x_{22} & x_{23} & \dots & x_{2p} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & x_{n3} & \dots & x_{np} \end{bmatrix} \quad , \quad Y_n = \begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{bmatrix}\\ y \in \{1,...,K\} \end{aligned}\]

In discriminant analysis, we assume that the conditional distribution of X to class Y is parametric and Gaussian \((X|Y = k \sim \mathcal{N}(\mu_{K},\Sigma_{K}))\)

Where:

  • \(\mu_{k}\): the centers of gravity of the conditional point clouds

  • \(\Sigma_k\): their variance-covariance matrix

Note

Then the probability density function (PDF) is:

\[\begin{aligned} f(x|Y=k) = \frac{1}{(2 \pi)^\frac{p}{2}|\Sigma_{k}|^{\frac{1}{2}}}exp\{ -\frac{1}{2}(x-\mu_k)^\intercal \sum\nolimits_{k}^{-1}(x-\mu_k)\} \end{aligned}\]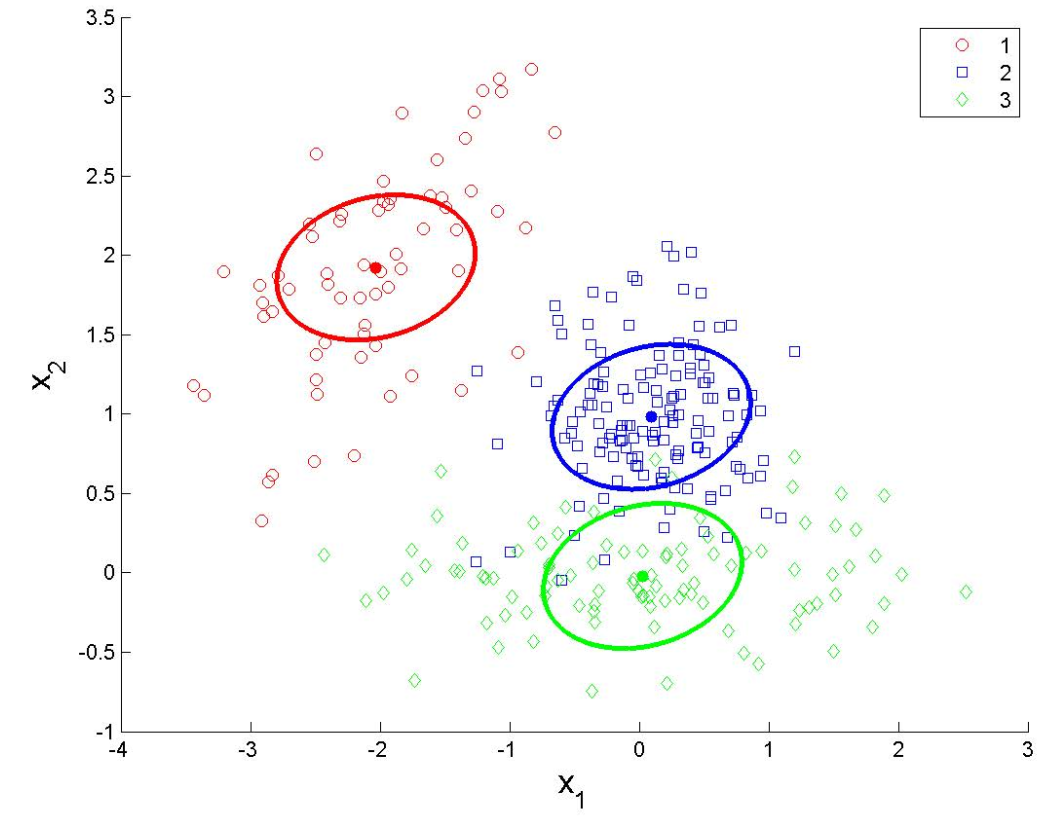

Linear discriminant analysis

Quadratic discriminant analysis

In training step, we want to find the classification rule \(g(x)\) that maximize the \(\mathbb{P}(Y = k | X = x)\). The Bayesian rule write as:

\[\begin{aligned} g(x) &= \mathbb{P}(Y = k | X = x) \\ &= f(x|Y=k) \mathbb{P}(Y=k)\\ &= log(f(x|Y=k)) + log(\pi_{k})\\ \end{aligned}\]

Maximum likelihood estimators

\[\begin{aligned} \widehat{\pi} &= \frac{n_k}{n} & \widehat{\mu_k} = \frac{1}{n_k}\sum_{i;y_i = k }^{}x_i\\ \widehat{\Sigma_k} &= \frac{1}{n_k}\sum_{i;y_i = k }^{}(x_i-\widehat{\mu_k})^\intercal (x_i-\widehat{\mu_k})\\ \end{aligned}\]

5.2 Linear Discriminant analysis (LDA)

We assume that K clusters have the same \(\Sigma\), \(\Sigma_k = \Sigma\) for k = 1,··· ,K. Now the likelihood is

\[\begin{aligned} f(x|Y=k) = \frac{1}{(2 \pi)^\frac{p}{2}|\Sigma|^{\frac{1}{2}}}exp\{ -\frac{1}{2}(x-\mu_k)^\intercal \sum\nolimits_{}^{-1}(x-\mu_k)\} \end{aligned}\]

take the log

\[\begin{aligned} log(f(x|Y=k)) &= \underbrace{- \frac{\pi}{2} log(2 \pi) - \frac{1}{2}log|\Sigma|} - \frac{1}{2}(x-\mu_k)^\intercal \sum\nolimits_{}^{-1}(x-\mu_k) \\ &= independent\ on\ k \\ &= - \frac{1}{2}(x-\mu_k)^\intercal \sum\nolimits_{}^{-1}(x-\mu_k) + constants \\ &= - \frac{1}{2}(x^\intercal \Sigma^{-1}x -2x^\intercal \Sigma^{-1}\mu_k+\mu^{\intercal}_k \sum\nolimits_{}^{-1}\mu_k) + constants \\ &= \underbrace{-\frac{1}{2}x^\intercal \Sigma^{-1}x} + x^\intercal \Sigma^{-1}\mu_k -\frac{1}{2} \mu^{\intercal}_k \sum\nolimits_{}^{-1}\mu_k + constants \\ &= same\ for\ all\ k \end{aligned}\]

We want to maximize \(g(x) = \mathbb{P}(Y = k | X = x) = log(f(x|Y=k)) + log(\pi_{k})\). So \(L_{k}(x)= x^\intercal \Sigma^{-1}\mu_k -\frac{1}{2} \mu^{\intercal}_k \sum\nolimits_{}^{-1}\mu_k + log(\pi_{k})\) is called linear discriminant function.

The posterior probabilities of the classes are calculated as follows:

\[\begin{aligned} \mathbb{P}(Y = k | X = x) = \frac{exp(L_k(x))}{\sum_{\ell=1}^{k}exp(L_\ell(x))} \end{aligned}\]

5.3 Quadratic Discriminant analysis (QDA)

We no longer assume that K clusters have the same \(\Sigma\), \(\Sigma_k = \Sigma\) for k = 1,··· ,K. Take the log likelihood of PDF of multivariate Gaussian distribution

\[\begin{aligned} log(f(x|Y=k)) &= \underbrace{- \frac{\pi}{2} log(2 \pi)} - \frac{1}{2}log|\Sigma_k|^{-1} - \frac{1}{2}(x-\mu_k)^\intercal \sum\nolimits_{k}^{-1}(x-\mu_k) \\ &= independent\ on\ k \\ &= - \frac{1}{2}log|\Sigma_k|^{-1} - \frac{1}{2}(x-\mu_k)^\intercal \sum\nolimits_{k}^{-1}(x-\mu_k) + constants \\ \end{aligned}\]

We want to maximize \(g(x) = \mathbb{P}(Y = k | X = x) = log(f(x|Y=k)) + log(\pi_{k})\). So \(L_{k}(x)= - \frac{1}{2}log|\Sigma_k|^{-1} - \frac{1}{2}(x-\mu_k)^\intercal \sum\nolimits_{k}^{-1}(x-\mu_k) + log(\pi_{k})\) is called quadratic discriminant function.

The posterior probabilities of the classes are calculated as follows:

\[\begin{aligned} \mathbb{P}(Y = k | X = x) = \frac{exp(Q_k(x))}{\sum_{\ell=1}^{k}exp(Q_\ell(x))} \end{aligned}\]

5.4 Limitations

  • LDA and QDA rely on statistical assumptions (normality of data and homogeneity of covariance matrices for LDA). These assumptions can be partially or totally violated in real datasets.

  • Even if LDA or QDA are considered relatively simple models, they can overfit on complex or noisy datasets.

5.5 Practical

Code 
library(caret)
library(MASS)
library(ggplot2)
Code 
train <- read.table(file="./data/synth_train.txt", header=TRUE)
head(train)
  y          x1        x2
1 2 -0.72221141 2.0044709
2 2 -0.92467912 0.4836693
3 2 -0.76602281 0.7943289
4 2 -0.07328948 0.9699291
5 1 -1.39291198 0.9996971
6 2 -0.20223339 1.3503319
Code 
train$y <- factor(train$y)
train_data <- data.frame(X1 = train$x1, X2 = train$x2, Class = factor(train$y))

ggplot(train_data, 
       aes(x = X1, y = X2, shape = Class, color = Class)) +
geom_point(size = 3) +
scale_color_manual(values = c("red", "blue"), name = "Class") +
scale_shape_manual(values = c(16, 17), name = "Class") +
labs(title = "Visualization of classes", x = "X1", y = "X2") +
theme_minimal() +
theme(legend.position = "top")

5.5.1 Quadratic Discriminant Analysis by Hand

Maximum likelihood estimators

\[ \widehat \pi_k = \frac{n_k}{n}, \qquad \widehat \mu_k = \frac{1}{n_k} \sum_{i; y_i=k} x_i,\qquad \widehat \Sigma_k=\frac{1}{n_k} \sum_{i; y_i=k}(x_i-\widehat \mu_k)^\top (x_i-\widehat \mu_k). \] We will estimate these parameters on these parameters on the training data.

n <- nrow(train_data)
# class 1
ind1 <- which(train_data$Class==1)
n1 <- length(ind1)
pi1 <- n1/n
mu1 <- colMeans(train_data[ind1,1:2])
sigma1 <- var(train_data[ind1,1:2])*(n1-1)/n1

# class 2
ind2 <- which(train_data$Class==2)
n2 <- length(ind2)
pi2 <- n2/n
mu2 <- colMeans(train_data[ind2,1:2])
sigma2 <- var(train_data[ind2,1:2])*(n2-1)/n2

We had the quadratic discriminant function

\[ Q_k(x)=-\frac 12 \log |\Sigma_k|^{-1} - \frac 12 (x-\mu_k)^\top \Sigma_k^{-1}(x-\mu_k)+\log \pi_k. \]

We have the new data \(x = (-1,1)\), then we calculate \(Q_1(x)\) and \(Q_2(x)\)

x = c(-1,1)
names(x) = c("x1","x2")
Q1 <- - 1/2*log(det(sigma1))-1/2*t(x-mu1) %*% solve(sigma1) %*% (x-mu1) +log(pi1)
Q2 <- - 1/2*log(det(sigma2)) - 1/2*t(x-mu2) %*% solve(sigma2) %*% (x-mu2) +log(pi2)

Q1
          [,1]
[1,] -1.940979
Q2
           [,1]
[1,] -0.9362387

We also know that the posterior probabilities of the classes are calculated as follows:

\[ \mathbb{P}(Y=k\vert X=x)= \frac{\exp (Q_k(x))}{\sum_{\ell=1}^2 \exp (Q_\ell(x))}. \]

Estimate the posterior probabilities for \(x = (-1, 1)\).

prob1 <- exp(Q1)/(exp(Q1)+exp(Q2))
prob1
          [,1]
[1,] 0.2680105
prob2 <- exp(Q2)/(exp(Q1)+exp(Q2))
prob2
          [,1]
[1,] 0.7319895

\(\mathbb{P}(Y=2/X=(-1,1)) > \mathbb{P}(Y=1/X=(-1,1))\) so we predict class 2 for \(x=(-1,1)\).

5.5.2 Quadratic Discriminant Analysis with caret

Now use the functions qda and predict to predict the class of the point \(x=(-1,1)\) and estimate their posterior probabilities. Check that you find the results obtained previously.

Training the model on the train data

qda_model <- train(Class ~ ., 
                   data = train_data, 
                   method = "qda")

Prediction of the point \(x = (-1,1)\)

X1 = -1
X2 = 1
x = c(X1,X2)
head(predict(qda_model, x, "raw"))
[1] 2
Levels: 1 2
head(predict(qda_model, x, "prob"))
          1         2
1 0.2679847 0.7320153

Splitting the dataset into training and testing samples

set.seed(1223)

train_index <- createDataPartition(train$y, p = 0.7, list = FALSE)
train_data <- train[train_index, ]
test_data <- train[-train_index, ]

Training the model on the training data

qda_model <- train(y ~ ., 
                   data = train_data, 
                   method = "qda")

Predictions on the test dataset

qda_pred <- predict(qda_model, test_data)

Model Evaluation - Performance Analysis on test dataset

qda_conf_mat <- confusionMatrix(qda_pred, test_data$y)
print(qda_conf_mat)
Confusion Matrix and Statistics

          Reference
Prediction  1  2
         1  6  1
         2  0 22
                                          
               Accuracy : 0.9655          
                 95% CI : (0.8224, 0.9991)
    No Information Rate : 0.7931          
    P-Value [Acc > NIR] : 0.01031         
                                          
                  Kappa : 0.901           
                                          
 Mcnemar's Test P-Value : 1.00000         
                                          
            Sensitivity : 1.0000          
            Specificity : 0.9565          
         Pos Pred Value : 0.8571          
         Neg Pred Value : 1.0000          
             Prevalence : 0.2069          
         Detection Rate : 0.2069          
   Detection Prevalence : 0.2414          
      Balanced Accuracy : 0.9783          
                                          
       'Positive' Class : 1

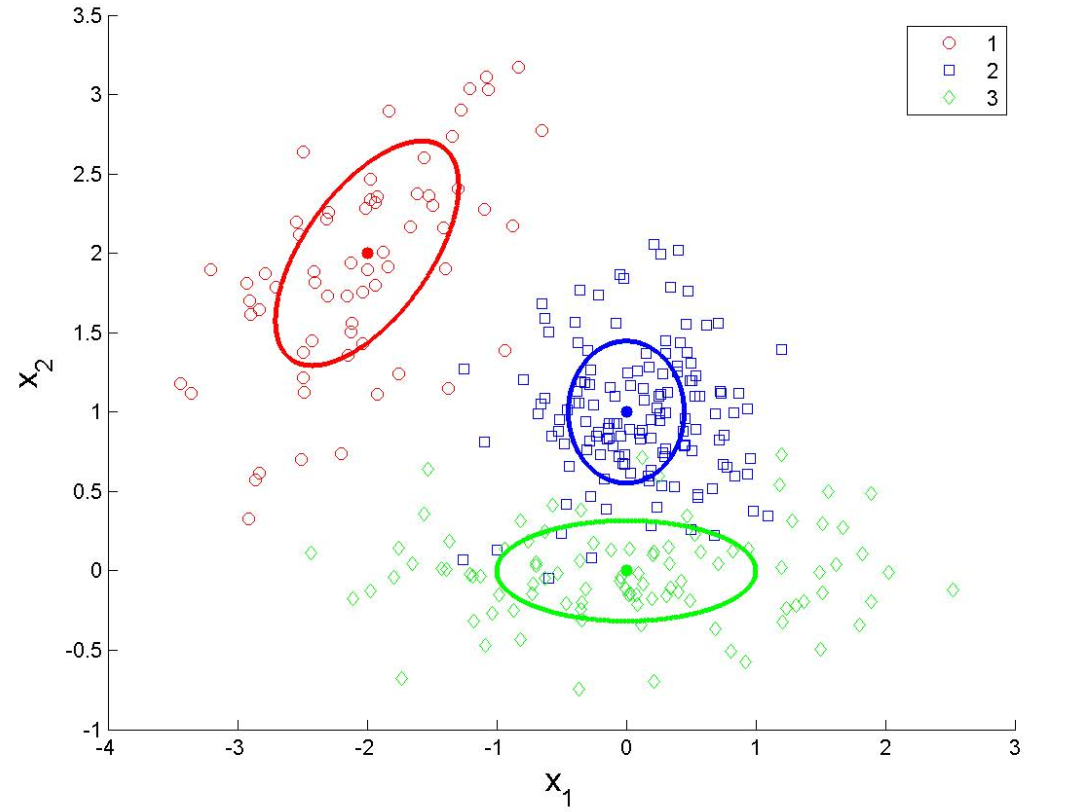
Visualizing the decision boundaries

grid <- expand.grid(x1 = seq(min(test_data$x1), max(test_data$x1), 
                             length.out = 100),
                    x2 = seq(min(test_data$x2), max(test_data$x2), 
                             length.out = 100))

# Decision boundary for QDA
grid$pred <- predict(qda_model, newdata = grid)

ggplot() +
    geom_point(data = test_data, aes(x = x1, y = x2, color = y), size = 3)+
    geom_tile(data = grid, aes(x = x1, y = x2, fill = pred), alpha = 0.3) +
    labs(title = "Decision boundary - QDA", x = "Variable 1", y = "Variable 2") +
    theme_minimal()

5.6 Practical 2

library(class)
library(caret)
library(FNN)
library(ggplot2)
library(readr)
library(gridExtra)
  1. Import the 500 images from the file numbers_train.txt.
dataTrain <- read.table("./data/numbers_train.txt", header=TRUE)
  1. Visualize the first 16 images.
# Function to convert a vector into a matrix 16 * 16
vector_to_matrix <- function(vec) {
  matrix(as.numeric(vec), nrow = 16, ncol = 16, byrow = TRUE)
}
plots <- list()
for (i in 1:16) {
  img_matrix <- vector_to_matrix(dataTrain[i, -1])  # Exclude the first column (label)
  img_df <- expand.grid(x = 1:16, y = 1:16)
  img_df$intensity <- as.vector(t(img_matrix))
  
 plots[[i]] =  ggplot(img_df, aes(x, 17-y, fill = intensity)) +
    geom_tile(show.legend = FALSE) +
    scale_fill_gradient(low = "black", high = "white") +
    coord_fixed() +
    theme_void() +
    ggtitle(paste("Image", i))
}

grid.arrange(grobs = plots, ncol = 4)

  1. Predict with the lda method the classes of the 500 images of the training set and calculate the learning error rate.
# Separate explanatory variables (pixels) and target variable (class)
Xtrain <- as.matrix(dataTrain[,-1])
Ytrain <- as.factor(dataTrain[,1])
train_data <- data.frame(Ytrain, Xtrain)

# Fit LDA on training set
lda_model <- train(Ytrain ~ ., 
                   data = train_data, 
                   method = "lda",
                   trControl = trainControl(method = "none")) # No cross-validation

# Predict on training set
y_pred <- predict(lda_model, Xtrain)

# Calculate error rate
error_rate <- mean(y_pred != Ytrain)
  1. Import the 500 images from the file numbers_test.txt.
dataTest <- read.table("./data/numbers_test.txt", header=TRUE)
  1. Now predict the classes of the 500 images of the test set and calculate the test error rate.
# Separate the explanatory variables (pixels) and the target variable (class)
Xtest <- as.matrix(dataTest[,-1])
Ytest <- as.factor(dataTest[,1])

# Predict on the test set
y_pred <- predict(lda_model, Xtest)

y_pred
  [1] 9 6 3 2 6 0 0 0 6 9 6 7 0 8 3 4 1 0 9 6 2 2 8 4 6 2 0 5 0 3 7 0 7 0 7 9 0
 [38] 7 0 7 0 2 1 0 7 1 0 4 9 0 8 5 2 0 0 6 5 9 8 0 9 0 0 4 0 9 1 2 2 1 8 3 7 2
 [75] 0 9 0 1 2 1 2 0 7 8 0 6 4 8 2 0 9 0 4 8 2 0 7 0 0 9 0 8 7 3 0 7 2 5 7 4 0
[112] 3 9 9 7 0 3 9 9 6 5 0 3 0 6 8 6 6 1 4 8 3 0 1 6 7 0 0 7 7 9 6 6 2 2 0 2 4
[149] 0 9 6 0 0 4 8 8 1 0 1 0 6 7 0 6 9 2 9 0 3 4 4 0 9 0 9 0 8 5 0 4 1 0 3 0 8
[186] 0 6 4 1 1 1 8 1 0 3 5 7 2 3 0 9 7 8 0 5 0 1 8 0 0 1 3 5 0 6 0 6 8 0 9 0 9
[223] 8 6 3 2 1 8 0 3 0 6 4 1 2 1 6 9 1 0 6 5 3 1 6 4 2 5 1 0 1 8 4 8 9 4 2 0 4
[260] 3 4 7 7 0 8 8 0 9 9 7 9 6 0 1 2 3 6 6 6 3 3 8 0 2 6 8 6 0 1 7 9 8 7 3 7 9
[297] 9 6 6 7 5 9 9 8 9 7 3 6 8 2 7 3 2 8 1 0 1 1 1 6 7 6 8 5 0 9 4 8 1 8 6 8 6
[334] 0 8 7 0 0 2 9 4 1 3 1 6 4 1 9 1 7 0 3 9 4 9 0 0 0 1 1 0 0 1 8 1 0 4 0 2 1
[371] 0 0 1 7 1 0 0 4 0 1 3 9 8 1 0 1 0 9 1 0 1 0 1 1 0 8 0 1 1 0 1 6 3 1 0 0 7
[408] 6 1 0 0 2 1 1 0 0 3 9 1 8 0 1 0 6 0 0 0 3 1 0 0 5 7 8 9 1 6 0 8 9 1 0 8 0
[445] 0 9 0 8 8 7 1 1 7 0 2 8 8 7 0 4 9 5 0 2 6 8 9 9 6 7 3 0 5 7 2 0 8 7 9 4 7
[482] 1 9 7 8 0 1 9 6 8 2 4 0 2 4 8 4 8 8 8
Levels: 0 1 2 3 4 5 6 7 8 9
# Calculate the error rate
error_rate <- mean(y_pred != Ytest)

# Display the result
cat("Training error rate:", error_rate * 100, "%\n")
Training error rate: 25.8 %